Fuzzy Logic
Boolean logic is represented either in 0 or 1, true or false but fuzzy logic is represented in various values ranging from 0 to 1. For example, fuzzy logic can take up values like 0.1, 0.3, 0.6, 0.8, 1, etc.
Let's take up a real-life example:
Let's say we want to recognize that the color of the flower is red or not.
In the following image, we can say that the flower is red.

In this following image, we can say that the flower is not red.

But what about this image, is it red or yellow?

Now, I am sure that you what to say it is partially red or 40% red or 60% red, etc. This type of ability we want to give it to the computers so that it can say how much of that feature is present.
The core idea behind Fuzzy logic is that it gives degrees of membership. It helps in recognizing more than simple true and false values. Using fuzzy logic, propositions can be represented with degrees of truthfulness and falsehood.
Range of logical values in Boolean and Fuzzy logic
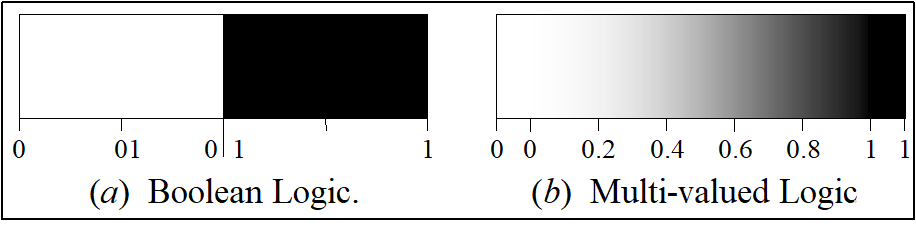
The traditional or classical set is also known as a crisp set. It contains objects which precise properties of membership. On the other hand, fuzzy set contains objects that satisfy imprecise properties of membership.
Therefore, Fuzzy logic is a superset of conventional (Boolean) logic that has been enhanced to fit the concept of partial truth where truth values lie between "completely true" and "completely false".
Linguistic variables and hedges
A fuzzy variable is sometimes called as linguistic variables. For example, "the tower is high", implies that linguistic variable "tower" takes the linguistic value as high.
While writing fuzzy rules in fuzzy expert systems, we will use fuzzy variables. Like for example,
IF the wind is strong
THEN sailing is easy
For a variable, the universe of discourse is the range of values it can take.
Linguistic Hedges
Linguistic hedges are the fuzzy set qualifiers which can be attached to linguistic variables. Linguistic hedges are the adverbs such as very, less, somewhat, more, etc.