side menu

Introduction to Linear Regression

What is Linear Regression?

Linear regression is a supervised machine learning approach for modeling a linear relationship between a dependent variable and one or more independent variables. In very simple words, it is an approach to create a straight line or a model from discrete values and generate an output which is continuous. It is used to solve classification problems.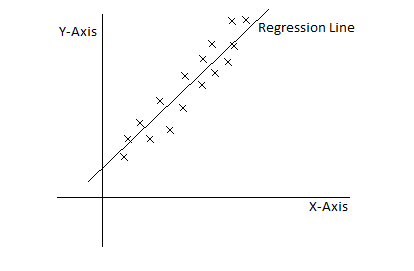

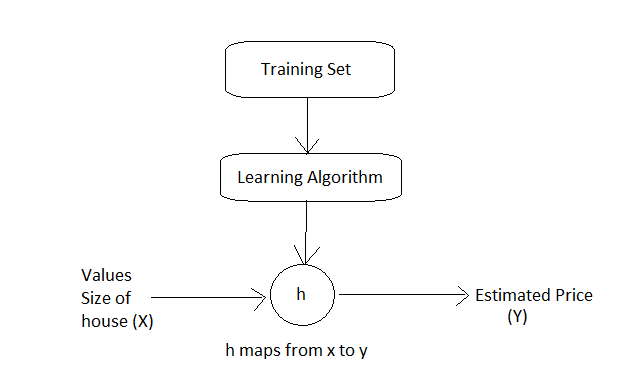
let's take an example sample training data set to predict the house prices.

Size in Feet(x)	Price($ in 1000s) (Y)
1000	450
1500	520
850	340
...	...

Linear Regression line is a straight line going through all points(may or may not overlap with points).The equation of a straight line is y=mx + c where m is the slope and c are the constant.In the linear regression model, slope will become the Weight and the constant will act as bias. The basic model will be ho=Weight*x + bias. where ,
W is the weight
b is the bias
x is "input" variable or features
y is "output" Variable or "target" variable
let's build a program in tensorflow.

import numpy as np
import tensorflow as tf
# declaring and initializing Weights and bias
Weight=tf.Variable([.3], dtype=tf.float32)
bias=tf.Variable([-.3], dtype=tf.float32)
# defining x and y parameters and making it placeholder since at first we don't know it's value
x=tf.placeholder(tf.float32)
linear_model=Weight * x + bias
y=tf.placeholder(tf.float32)
Now, we need to predict Weight and bias. To predict the Weight and bias, we will use the training data.

Cost Function

A cost function helps us to fit the best straight line to our data.It is also called Squared error function.It is denoted by J, J(Weight,bias)

`J(Weight,bias)=(1/(2m))\sum_{i=1}^m (h_o(x^i) -y^i)^2`

We can measure the accuracy of our hypothesis function by using a cost function. This takes average difference of all results of the hypothesis with inputs from x's and the actual output y's
`h_o(x^i)` is the predicted value and
`y^i` is the actual value.
therefor this function is called "Squared error function" or "mean squared error". The mean is halved `(1/2)` as a convenience for the computation of the gradient descent, as the derivative term of the squared function will cancel out `(1/2)` term.
Now the objective is to minimize this to find accurate value of Weight and bias. In order to achieve all this in tensorflow, we can use tensorflow library functions

# In order to calulate loss
loss=tf.reduce_sum(tf.square(linear_model - y)) # calculates sum of the squares
# optimizer
optimizer=tf.train.GradientDescentOptimizer(0.01)
train=optimizer.minimize(loss)

tf.reduce_sum(input_tensor) : This function adds the elements across dimensions of a tensor.So, it acts as summation `\sum_{}`
tf.train.GradientDescentOptimizer() : This function is an optimizer which uses the gradient descent algorithm.Gradient descent is a first-order iterative optimization algorithm for finding the minimum of a function.

Training data and Training loop


# training values
x_trainingData=[1,2,3,4]
y_trainingData=[0,-1,-2,-3]
# training
init=tf.global_variables_initializer() # To initialize all Variable
sess=tf.Session()
sess.run(init) # reset values to wrong
# loop
for i in range(1000):
    sess.run(train,{x:x_trainingData, y:y_trainingData})

while training we have to feed all training data repeat this task

Calculate training accuracy


curr_Weight, curr_bias, curr_loss=sess.run([Weight, bias, loss],{x:x_trainingData, y:y_trainingData})
print("W: %s b: %s loss: %s"%(curr_Weight, curr_bias, curr_loss))
We need top get weight, bias and loss, and print accordinly.

Final Program


import numpy as np
import tensorflow as tf
# declaring and initializing Weights and bias
Weight=tf.Variable([.3], dtype=tf.float32)
bias=tf.Variable([-.3], dtype=tf.float32)
# defining x and y parameters and making it placeholder since at first we don't know it's value
x=tf.placeholder(tf.float32)
linear_model=Weight * x + bias
y=tf.placeholder(tf.float32)
# In order to calulate loss
loss=tf.reduce_sum(tf.square(linear_model - y)) # calculates sum of the squares
# optimizer
optimizer=tf.train.GradientDescentOptimizer(0.01)
train=optimizer.minimize(loss)
# training values
x_trainingData=[1,2,3,4]
y_trainingData=[0,-1,-2,-3]
# training
init=tf.global_variables_initializer() # To initialize all Variable
sess=tf.Session()
sess.run(init) # reset values to wrong
# loop
for i in range(1000):
sess.run(train,{x:x_trainingData, y:y_trainingData})
curr_Weight, curr_bias, curr_loss=sess.run([Weight, bias, loss],{x:x_trainingData, y:y_trainingData})
print("W: %s b: %s loss: %s"%(curr_Weight, curr_bias, curr_loss))


Output


W: [-0.9999969] b: [ 0.99999082] loss: 5.69997e-11